Bahas Soal Matematika   »   Turunan   ›  

Carilah \( \frac{dy}{dx}\) untuk fungsi implisit \(4x^2y - 3y = x^3 - 1\).

Pembahasan:

Cara 1: Modifikasi fungsi implisit sehingga menjadi fungsi eksplisit sebagai berikut.

Kemudian dengan menggunakan rumus turunan pembagian, kita peroleh turunan dari fungsi eksplisit di atas sebagai berikut:

Cara 2: Turunkan kedua ruas persamaannya terhadap \(x\) secara bersamaan, yakni

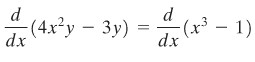
Untuk mencari turunan pada ruas kiri persamaannya, kita bisa memakai aturan perkalian, sedangkan untuk ruas kanannya bisa menggunakan rumus dasar turunan. Kita peroleh berikut ini:

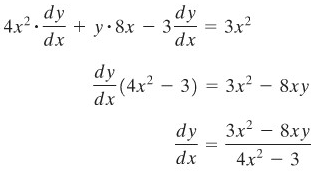
Walaupun jawaban ini kelihatan berlainan dari jawaban yang diperoleh dengan cara pertama, tetapi keduanya adalah sama. Untuk membuktikannya, gantikan \( y = \frac{x^3 - 1}{4x^2 - 3}\) dalam persamaan untuk \(\frac{dy}{dx}\) yang baru saja diperoleh,

Jadi, kesimpulannya adalah baik cara 1 maupun cara 2 menghasilkan jawaban sama. Pertanyaannya adalah menggunakan cara yang mana? Dalam penerapannya, terkadang dengan menggunakan cara 1 saja sudah cukup, tetapi terkadang juga akan dijumpai soal di mana akan jauh lebih mudah menggunakan cara yang kedua.